Introduction

Game theory is a powerful tool that can be used to understand the dynamics of competitive interactions between players. In the context of search engine optimization (SEO) & marketing, game theory can help us analyze the strategic decisions made by websites competing for higher rankings on search engines like Google.

I decided to write this as I wanted to show how unique strategies can be used to gain a competitive advantage. Given that we have peak maturity in the SEO & marketing industry, it is important to think outside the box and come up with innovative strategies to stand out from the competition.

Players and Strategies

I want to introduce you to a hypothetical scenario involving two players:

• Cub Digital (Player 1)
• Competitor (Player 2)

Both players are competing and trying to come up with a marketing strategy, trying to optimize their websites to rank higher on search engines.

Each player has two strategies to choose from:

• Common SEO & Marketing Practices (C): This strategy involves using well-known SEO & marketing techniques that are widely used in the industry. These practices are effective but may not provide a competitive advantage due to high competition.

• Unique SEO & Marketing Practices (U): This strategy involves using innovative and unique SEO & marketing techniques that are not commonly used by competitors. These practices may provide a competitive advantage but come with higher risks and uncertainties.

Players:

• Cub Digital (Player 1)
• Competitors (Player 2)

Strategies:

• Common SEO Practices (C)
• Unique SEO Practices (U)

Payoff Matrix

The payoff matrix represents the potential outcomes for Cub Digital and its competitors based on their chosen strategies. For simplicity, let's assume the payoffs are:

• If both Cub Digital and Competitors choose C (Common SEO Practices), they split the market evenly, with moderate returns due to high competition.
• If Cub Digital chooses U (Unique SEO Practices) while Competitors choose C, Cub Digital gains a competitive advantage and higher returns.
• If both choose U, they split the unique market, which is less saturated but still provides some advantage over common practices.
• If Cub Digital chooses C while Competitors choose U, Cub Digital gets lower returns due to high competition in common practices while Competitors gain an advantage.

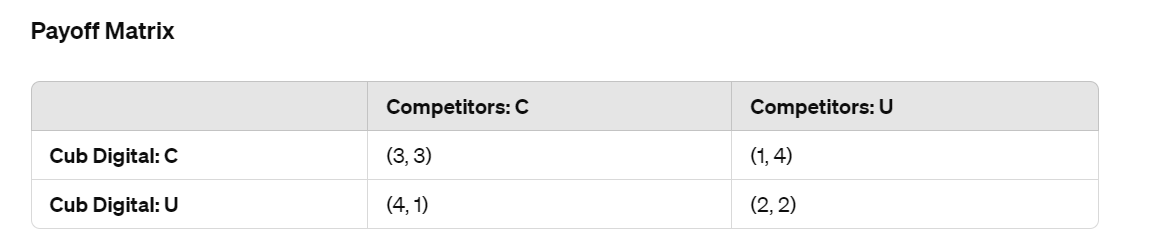
Let's assign the following payoffs:

• C, C: (3, 3)
• C, U: (1, 4)
• U, C: (4, 1)
• U, U: (2, 2)

Here, the first number in each pair is the payoff for Cub Digital, and the second number is the payoff for the Competitors.

Showing expected payoffs

Finding Nash Equilibrium To find the Nash Equilibrium, we need to identify the strategy pairs where no player can improve their payoff by unilaterally changing their strategy.

An equilibrium point in a finite n-person game is a point in the space of mixed strategies from which no player, knowing the strategies of the others, has any incentive to deviate unilaterally.

Nash, J. (1950). Equilibrium Points in N-Person Games

Cub Digital chooses C:

• If Competitors choose C: Cub Digital's payoff is 3.
• If Competitors choose U: Cub Digital's payoff is 1.
• Given Competitors' choice, Cub Digital would prefer C (payoff 3) over U (payoff 1) if Competitors choose C.

Cub Digital chooses U:

• If Competitors choose C: Cub Digital's payoff is 4.
• If Competitors choose U: Cub Digital's payoff is 2.
• Given Competitors' choice, Cub Digital would prefer U (payoff 4) over C (payoff 1) if Competitors choose C.

Competitors choose C:

• If Cub Digital chooses C: Competitors' payoff is 3.
• If Cub Digital chooses U: Competitors' payoff is 1.
• Given Cub Digital's choice, Competitors would prefer C (payoff 3) over U (payoff 1) if Cub Digital chooses C.

Competitors choose U:

• If Cub Digital chooses C: Competitors' payoff is 4.
• If Cub Digital chooses U: Competitors' payoff is 1.
• Given Cub Digital's choice, Competitors would prefer U (payoff 4) over C (payoff 1) if Cub Digital chooses U.

Finding Nash Equilibrium

To find the Nash equilibrium, we need to identify a strategy pair where neither Cub Digital nor its competitor has an incentive to unilaterally change their strategy.

Given that the competitor always chooses C, we need to determine the best response for Cub Digital when the competitor chooses C:

If Cub Digital chooses C, the payoff is (3, 3).
If Cub Digital chooses U, the payoff is (4, 1).

Cub Digital will choose the strategy that maximizes its own payoff. In this case, if the competitor always chooses C, Cub Digital will choose U because the payoff (4) is greater than the payoff for choosing C (3).

Therefore, the Nash equilibrium, given that the competitor always chooses C, is:

Cub Digital: U, Competitor: C with the corresponding payoffs of (4, 1).

Conclusion

This article demonstrates how game theory can be applied to SEO & marketing strategies to analyze competitive interactions between players. By understanding the strategic decisions made by competitors and identifying the Nash equilibrium, businesses can make informed decisions to gain a competitive advantage in the market.

We can see that by choosing unique SEO & marketing practices, there is the potential to outperform competitors and achieve higher returns. However, this strategy comes with risks and uncertainties, and businesses must carefully evaluate the trade-offs between common and unique practices to maximize their success.

Of course this article doesn't answer exactly what the unique SEO practices are, that is something that we will explore in future articles. Stay tuned for more insights on how to apply game theory to SEO & marketing strategies!